Ein Sprung ins Universelle

Forschende der Physik lieben Klassifizierungen: Bosonen und Fermionen, Leiter und Isolatoren - jeder Zweig der Physik hat seine bevorzugten Etiketten. Wenn die Forschung zeigt, dass sich physikalische Systeme mit scheinbar wenig Gemeinsamkeiten ein solches Etikett teilen (d. h., es gibt einen Standpunkt, von dem aus sie trotz ihrer Besonderheiten in ähnlicher Weise beschrieben werden können), kann die Klassifizierung sehr wirkungsvoll werden. Die universellen Klassifizierungen können dann eine besondere Erwähnung als mächtiges Kategorisierungsinstrument verdienen.

Das Konzept der Universalität ist eng mit dem kritischen Verhalten verbunden. In der Thermodynamik bezeichnen kritische Punkte Bedingungen (Druck und Temperatur), bei denen klare Grenzen zwischen Phasen - z. B. Flüssigkeit und Dampf - nicht mehr existieren. Forschende wissen seit einiger Zeit, dass sich physikalische Systeme, die sehr unterschiedlich sind, in der Nähe kritischer Punkte überraschend ähnlich verhalten können. Aber was bedeutet "ähnliches Verhalten" in diesem Zusammenhang? In der Nähe von kritischen Punkten werden die Veränderungen einiger Eigenschaften eines gegebenen physikalischen Systems durch Potenzgesetze mit sogenannten kritischen Exponenten erfasst. Wenn verschiedene Systeme in der Nähe eines kritischen Punktes mit demselben Satz von kritischen Exponenten beschrieben werden können, bedeutet dies, dass sie dasselbe kritische Verhalten aufweisen und zur selben Universalitätsklasse gehören. Die Forschenden zeigten außerdem, dass es Skalierungsgesetze gibt, die einfache mathematische Beziehungen zwischen kritischen Exponenten herstellen.

Die Universalität ist für Physikerinnen und Physiker deshalb so attraktiv, weil sie die Untersuchung komplexer Systeme vereinfacht, da detaillierte Kenntnisse der mikroskopischen Wechselwirkungen oft nicht erforderlich sind, um das makroskopische Verhalten in der Nähe kritischer Punkte vorherzusagen; das Verständnis der Symmetrieeigenschaften und der Dimensionalität des Systems kann ausreichen. Im Falle von Gittersystemen mit Wechselwirkungen in endlicher Reichweite bedeutet Universalität, dass die kritischen Exponenten unabhängig von Änderungen im Wechselwirkungsbereich oder in der Gitterstruktur sind.

Zahlreiche experimentelle Daten zeigen, dass viele verschiedene physikalische Systeme in wenige Universalitätsklassen eingeteilt werden können, und es gibt genaue empirische Schätzungen der kritischen Exponenten für jede dieser Klassen. An der theoretischen Front haben sich die Forschenden bemüht, ihre Modelle zu verfeinern, um ihre abgeleiteten Exponenten mit den experimentellen Werten in Einklang zu bringen. Theoretische Studien über Universalität und kritische Skalierung waren jedoch meist auf homogene Systeme beschränkt, d. h. auf physikalische Systeme, bei denen sich die mikroskopischen Bestandteile auf den Seiten eines regelmäßigen Gitters befinden.

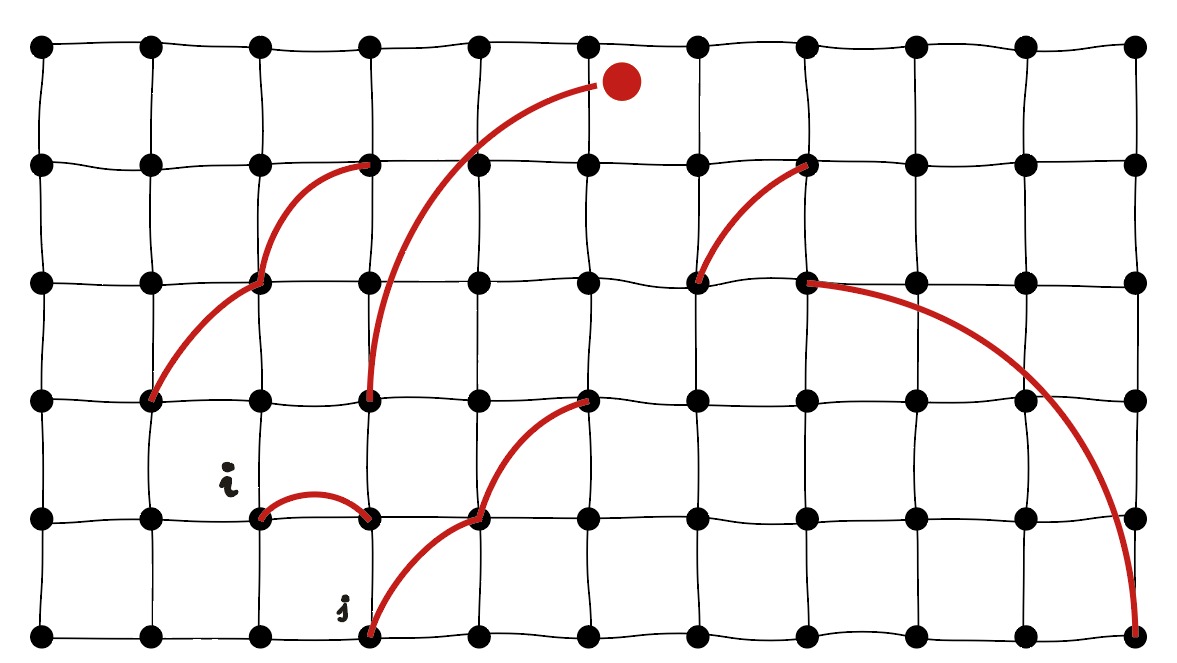
In einer kürzlich in Nature Communications veröffentlichten Arbeit untersuchten Professor Nicolò Defenu vom Institut für Theoretische Physik am D-PHYS und Mitarbeitende der Universität Heidelberg in Deutschland die Universalität von Skalierungsphänomenen in einem prototypischen nicht-homogenen System, einem so genannten langfristig verdünnten Graphen mit einer Dimension, die sowohl ganzzahlige als auch nicht-ganzzahlige Werte annehmen kann. Auf diesem Graphen simulierte das Team ein mikroskopisches Modell, den Self-Avoiding Random Walk (SARW), der in der statistischen Physik als einfaches Beispiel für universelles Verhalten bekannt ist. Die Forscher berechneten den kritischen Exponenten für die SARW als kontinuierliche Funktion der Dimension und fanden Hinweise auf eine universelle Skalierung in der Grafik. Tatsächlich zeigen ihre numerischen Simulationen eine gute Übereinstimmung mit theoretischen Vorhersagen des universellen Verhaltens, die aus Skalierungsargumenten abgeleitet sind, die nicht auf Annahmen über die Graphenstruktur beruhen. Diese Übereinstimmung gilt für einen breiten Bereich ganzer und nicht ganzer Dimensionen.

Defenu und seine Mitautoren diskutieren offen die Vermutungen, die ihrer Studie zugrunde liegen, die sie als einen Schritt in einer längerfristigen Untersuchung sehen. Sie sind zuversichtlich, dass diese Arbeit zur Wiederbelebung der theoretischen Forschung über Universalität in komplexen physikalischen Systemen beitragen wird. Auch glauben sie, dass diese Forschungsrichtung ein wichtiges theoretisches Gegengewicht zu experimentellen Quantensimulationen komplexer inhomogener Systeme sein wird, wie sie mit in optischen Pinzetten eingeschlossenen Rydberg-Atomen realisiert werden können. Aus einer entfernteren Perspektive betrachtet, kommen inhomogene Systeme in so unterschiedlichen Bereichen wie der Epidemiologie und Informationsnetzwerken vor, so dass ein tieferes Verständnis des universellen Verhaltens dieser komplexen Systeme weit über die Physik hinaus Auswirkungen haben dürfte.

Übersetzung: Kilian Kessler